The ancient Greeks and Romans rightly believed that magic were invented by the Persians. The 1st-century Roman writer Pliny the Elder (CE 23 – AD CE) has written that magic was first discovered by the Persian prophet Zoroaster around the year 1700 BC.
Indeed magic is a word derived from magos (Greek) which was derived in turn from the Persian word magus (plural magusan or magusha) or mogh (plural moghan or moghha) which are the names for Zoroastrian priests. In ancient times, Persia (now Iran) was a large empire and ruled much of the civilized world. The moghs or magus were the keepers of knowledge and science. Among their many duties were healing, keeping time, and predicting eclipses. The Greeks, then still governed as city states rather than a unified country, could not understand the means of the magus’s success and consequently attributed it to supernatural powers. From this belief, the word magus, meaning priest, gradually entered the Greek language, and then other European languages. The magus, for the Greeks, referred to someone capable of performing magic and feats of great power.
Considering the oldest magic book in the world, two titles stand out the Discoverie of Witchcraft and the Powers of Numbers. The Discoverie of Witchcraft1 is a skeptical book written by an Englishman in the name Reginald Scot in 1584. The purpose of the book was to expose witchcraft, since still people were being accused of witchcraft and put on the stake at the time in the Europe. He tried to show that some of the technique the witches do is by natural means and not by supernatural ways.

The Power of Numbers2 is written by an Italian mathematician between 1496 and 1508 CE which contains some mathematical problems and some mathemagic and magic.
Both of the authors were living at a time where there was burst of translation of Persian and Arabic books on science, mathematics, and philosophy into Latin language which started during the crusader wars and was continuing afterwards.
I would like to review the oldest magic book in the world which is five centuries older than those two books. It is titled Tuhfat al-Ghraib (The Gift of Wonder), written in Persian by Muhammad ibn Ayyub Alhaseb Tabari. This book is believed by various scholars to have been written sometime between 978 and 1135 CE. Jalal Matini, the editor of the most recent edition of the book, 3 sets the date of writing before 1107 CE. Its age clearly makes it a highly important record for conjuring history.
The author Tabari was born in the city of Amol in the Tabarestan (Mazandaran) province of Iran (about 112 miles northeast of Tehran). Tabari was a scholar who wrote eleven known books and treatises (others may remain to be discovered) on mathematics, geometry, astronomy and the astrolabe. He was a renaissance man before the age Renaissance. From evidence in The Gift of Wonder it seems he was a rationalist with little or no belief in metaphysics and the supernatural.
The Gift of Wonder concerns itself with strange and unexplained phenomena. Tabari tries to explain these things through logic and natural laws, and in this effort he on occasion discusses secrets of conjuring and mentalism as an art and entertainment form.
The Gift of Wonder is an encyclopedia of the applied sciences of its time. The information Tabari presents in its pages was the best and most current for his time. The rational outlook of people like Tabari over the last millennium has expanded the frontiers of science and resulted in scientific progress and the advancement of knowledge. Some of the information Tabari includes remains valid. Various experiments can be repeated and explained by principles of today’s science. Others must be considered folklore and superstition that Tabari did not recognize as such. It is important to note that it show us how the people of his age spent their time, how they amused themselves; and it provides a measure of the level of education and the state of the sciences in Iran of a millennium ago.
The Gift of Wonder is divided into thirty-four chapters. It attempts to collect and elucidate on weird and unexplained phenomena, drawn from oral and written sources. These included scientific, natural and geographical marvels. One interesting aspect of the book is that Tabari writes about subjects and uses words still taboo in many Islamic countries, such as sex, intercourse, wine selection, aphrodisiacs, impossibility of miracles, and artificial method to repair of virginity.
At the beginning of the book he states:
“This book is a compilation of words of thinkers, philosophers, tourists and travelers on rare and strange and interesting and weird things, and on strange sciences and weird properties that intelligent and smart people have seen, learned and tested, and what has been received them.”
Magic squares were invented by the Persians and can be seen in the many of books on mathematic written before Tabari. He also presents two magic squares wherein the numbers add up to nine and fifteen.

In Chapter seven we encounter a topic commonly related to conjuring in early works: Invisible inks. Besides the usual transparent inks that become visible by heat, water or chemicals, there is one that becomes readable when ash is rubbed on the paper, and a related preparation for making writing appear on the hand. Both techniques are still well-known and used today by magicians. Another piece of information of interest to conjurers is how one can open a sealed envelope without breaking the seal.
Chapter ten and chapter twenty are the two chapters that are completely devoted to the magic tricks, amusements and entertainments and we include the whole chapters and select some of the magic tricks from other chapters [Clarifications and notes by me appear within square brackets.] Note how Tabari approaches the topic of these scientific novelties and practical jokes. They are treated strictly as a form of entertainment, and their explanations are intended to educate and to dispel superstition, an intention Tabari pursues throughout the book.
Chapter Ten
“On playing games, tricks and nice, smart amazements”
If you want to amaze [people], make a wooden bird and fix it on a wooden stick and make it rotate quickly, so that it will be
amazing. Take the plant called rye [rye is the usual translation, but could be different plant] and there has black branches. You take that branches off it, and make a wooden bird. Make a hole underneath it and take a stick the size of the hole and make sure you can put the stick into the hole. Take it out, put a bit of wax on it and put the bird onto the stick; then move your lips for a moment, showing that you are saying magic words. If you want [the bird] to rotate, secretly make your finger wet and rub it on the stick, so that it gets wet. When the stick gets wet, the bird will rotate around on the stick due to the [spiral or twisted] grooves that are in the wooden stick. When you notice that the rotation of the wood has ended, wait a moment, then say, “You, bird, rotate again, in reverse.” If the wood has dried, it will rotate in reverse. And you will have done two tricks smartly. Magicians call this wood “screw.”
If you want to do secret, amazing tricks, take two bowls full of water: one bowl of clear water and one bowl of dew which is collected at night from the leaves of reeds. Take both bowls in your hand: the one containing the clear water in your left hand, and the one containing dew water in your right hand. Put both in the sunlight. Pour the clear water into the dew gradually and patiently, and do not hurry, so that whatever is poured into that bowl of dew water, sunshine delicately removes from it until that bowl is empty of the dew water and the bowl is full and has not increased. [Theoretically, this is because the dew is like distilled water and has different evaporation rate than the common drinking water which has impurities and therefore evaporates a bit faster than the drinking water. However, it is doubtful if this experiment works.]
Also, if you want to move an egg with the dew you collected from reed leaves, you should [make a hole and] clean the inside of the egg and should dry it and the hole should be narrow. That dew water should be put into the egg and you instill a bit of violet oil in it and seal the egg with a piece of wax and put it in sunlight, so that the water is warmed. The egg will start moving due to that water, depending on the strength of the sunshine. And this is an amazing thing. [Similar trick is described in J. Prevost book titles La premiere partie des subtiles, et plaisants inventions, 1584, Lyobs, p. 43]
If you want to gather whatever insects are in the house, you should put salted fish in the house. All the insects gather around the fish. Also if we want to move and make a ring jump and run on the ground, order a hollow ring to be made and put mercury inside it and fix a gemstone on it tightly, so that mercury does not come out. When you place the ring in a warm bathhouse, it will move and goes from one side to the other side. If it is placed near fire, it still goes around and moves.
Also, if you want a roasted fish to move, you should place a bit of mercury inside the fish gut when is taken out [of the oven], and the exit for the mercury should be sealed. After leaving it for an hour, the fish starts moving.
Also, if you want to grow something instantly, you should take Indian hemp seed and take the skin off, and put it in the ground and water it, and it will grow instantly.
Also, if you want [to grow something instantly] soak an unripe pistachio nut in milk for three days. The milk should be fresh. Then take it and dry it in the shade. If you want it to grow quickly, when you water it, it will grow instantly.
Also, if they want to turn the hair or the beard of a person which was black to white, burn sulfur under the hairs. It will turn white. And if you want to make it black again, you should wash it with sour vinegar to make it black.
And also, if they want to prevent someone from sleeping, you should rub a bit of green vitriol [iron sulfate] in his nostrils [so that he] does not sleep. And if you want [him] to go to sleep, you should put olive oil in water and stir it to mix it, and then rub it in his nostrils. Then wash it with water; [he] will go to sleep instantly and will sleep well.
Also, if you want to make the hand of a person black at the time of hand washing [for eating] at parties, grind some of alum and mix it with soap root and give it to him to wash [his] hands; it will make his hands black.
And if someone takes Indian faba—and this is a green wood, more whitish—and makes two shapes of people from mud or paste and puts that wood between them and puts them into the furnace, a sound will come from that furnace like the crow of arooster. It is said that, if you throw these shapes of people in warm water, the same sound still comes out.
And also, if you grind common fumitory [an herb] and put it through a sieve and give it to a person to smell, he will pass gas.
Also, if you put ant’s eggs into date wine and give this to a person to drink, it causes that person to pass gas.
Also, if you want to turn one side of a rose petal white, you should separate the petals and spread them on the back of a sieves and burn sulfur underneath; one side becomes white and the other side stays red.
Also, if you want to put an iron needle on the water in such a way that it does not sink in the water, you should rub wax all over it and gently put it on the water. It will stay [floating] and does not sink.
Also, if you grind sulfur and add it to old wine, whoever drinks that wine, his hair will turn white.
Also, if you smash fresh lentil and mix it with henna thorn and rub [it on white hair], the white hair will turn to red, like blood.
And also, if the ground dried leaves of beans in water are given to a person to drink, the person instantly will pass gas.
Also, if a person eats a lot of roasted dried fava bean, and drink warm water afterwards again, it causes the person to pass gas.
If you take limestone and put uncooked eggs on it, and then pour water on it, the egg will cook from its heat. And if you place them in a bucket and hang it in a well, the limestone absorbs the vapors of the well to cook the egg, and this is interesting.
And if you make a snake from wood and put some pieces of wild celery where the [snake’s] fangs are, whoever touches it will feel as if the snake sunk in its fangs and bit him in such a way that [he] could not tolerate, unless you rub it with oil, until the pain goes away. [Wild celery is poisonous and causes pain when brought in contact with the skin.]
And if you take two big rooster feathers when they have fallen from its back and put them in a bathhouse water vessel, whoever pours that water over [his] head, his penis will harden instantly.
If your paint green vitriol [iron sulfate] in vinegar on iron and dry it in the sunshine, it will look so red it seems it has been reddened in fire. If you take it in hand, nobody will notice it, and will think it is hot iron, and this is very interesting.
And if you want, take some bran, mix it with some alum and give it to someone to wash [his] face with and his face will turn black. And this is enough. God knows best.

In Chapter Twelve Tabari describes ways of writing a letter in which the reply appears instantly on the paper.
In chapter thirteen the reader is told how to condition snakes to crawl from a basket when a bell is rung, and how a snake is trained to dance to the sound of a flute by feeding it only when the flute is played.
Chapter Fourteen is titled: “On making fine fires and doing things related to the fire.” In it stunts involving fire are discussed, such as producing fire in unusual ways, using chemicals, making fire-resistant cloth, applying fire to the body without suffering burns, producing flames on the fingertips and putting fire on tongue without injury, and creating an eternal flame. He also explains how pictures of two human heads can be drawn on a wall, after which sal ammonic is put in the mouth of one and sulfur in the mouth of the other. When a lamp is brought near the mouth of the first, it is extinguished, and when brought to the mouth of the second, it is relit.
Chapter Twenty is the second chapter of particular interest to magicians. In it Tabari discusses mathematical, algebraic and geometrical puzzles and games, including some feats of mathemagic and mentalism, used as entertainments at parties and gatherings of the time. The entire chapter is presented here, with my notes and clarifications inserted in square brackets.
Chapter Twenty
On doing fine and smart games at parties and other places
And if you like to play a smart number games where people are gathered, we will mention some of this sort:
When a ring or something else is hidden amongst a group and you want to find out who has it, one should ask the person [who has given his ring to another person to hide] to count from his right side secretly to the person who has the ring, and when he has counted, ask him to add half of that number to it. Once the number has been added, ask if the result is a fraction; that is, a number and a half? Then [if it is a fraction] keep a one [in your mind], and if not, do not keep a one [in your mind]. If it has half a number, then [tell him to] add another half to it to make it a round number. Then, for the second time tell him to add half of that number to the result. Once it has been added, ask if it is fraction. If he says it is a fraction, then add two to the number you had kept [in your mind], whether you had one or not, and tell him to make the number round again, and when he does it, tell him to deduct nine from it. If he says he deducted it, tell him to continue deducting another nine from it, until nine can no longer be deducted from it. For each instance where nine was deducted, add four to the numbers you kept [in your mind], whether you kept a number or not, and then look at the result. Whatever number you obtain, count from his right side to arrive at the man who has the ring.
An example: If there are fifteen people in a party, one of them has hidden a ring, and it is the seventh person [to his right] who has it, and amongst that group nobody knows who has the ring, except the one who has hidden the ring [and the one who holds it]. So I said “Count,” to that person; he said, “I have counted.” I said, “Add half of the number to it”; he said, “I have added it.” I asked, “Is it fraction?” He said, “Yes.” I kept one number [in my mind] and said, “Make the number round”; he said, “I have.” I said, “Add half the number to it again”; he said, “I have added.” I asked, “Is it a fraction?” He said, “Yes.” I added two to the one [in my mind] to make three and kept it, and said, “Make the number round”; he said, “I have.” I said, “Deduct nine from it”; he said, “I have deducted.” I added four to the three I had kept [in mind] to make seven. I said, “Deduct nine from it”; he said, “I cannot deduct nine.” So it was evident the seventh person had the ring.
Another type: If there are a group of people at a party, one of them chooses a number and says this number is less than ten. I want you to add a number to it, so that it totals ten. Then subtract one from the number you added to make it to ten, and then subtract another five from that number. So we take number ten, because I said to make it ten, and if said twenty, we considered twenty [i.e. a number above ten can be worked with]. So we took one, because he said to take it, and then another five, totaling sixteen. I asked him what remained; he said two. We added eight to it to make it to ten. From the eight we subtract the one we had taken before, so seven is left. We subtract another five that we had taken before, so two is left. We told him, “ this is the number you had,” and all is like that.
[In this trick, the magician tells a spectator to think of a number less than ten and add a number that brings the thought-of number to ten. Then deduct one from the number you added to it, followed by another five and tell me what remains. If he says it is two, it is evident that he has thought of two.
Another type: There gathered a group in a party and one of them says that we have two numbers between two of us with the sum of ten. Find what number each of us has. The way to calculate it is that we consider the number ten the base number, and multiply it by ten to make it one hundred and consider it the base number squared. Then tell one of them to “Multiply your number by two,” and tell the other person to multiply it by ten. “And add both numbers and tell me what it is.” When he says what number it is, we deduct that number from one hundred, what remains we divide by eight. The result is the number the first person had, and what remains from ten is the number the second person had.
An example: He told us it is ten; this is the base number. We multiplied the base number by ten to obtain one hundred, which is the base number squared. “Then we said multiply your number by two”; he said “I did.” And told the other person, “Whatever you have got multiply by ten.” He said, “I did.” I said, “[Add both numbers and] tell me what the number is” He said, “It is seventy-six.” I deducted it from one hundred. Twenty-four remained. I divided it by eight and the result was three. It was known that the first man whom I told, “Multiply your number by two,” had [picked the] number three, and the remainder of three from ten is seven. This is the number of the other man whom I told, “Whatever you have multiply by ten,” and it was clear he had number seven.
[This trick can be used to reveal a two chosen cards where the sum of the two numbers are ten or less.]
[Another type:] If, among a group, three people say, “The sum of numbers we have is twelve; find out how many each of us has,” we call twelve the base number, and then multiply twelve by twelve to get one hundred and forty-four and call this base number squared and keep it. Then tell one person, “Whatever you have, multiply by two,” and tell the other person, “Whatever you have, multiply by eleven,” which is one less than twelve, and tell the third person, “Whatever you have, multiply by twelve.” When they have done this, we ask what the result is. When they have told us, we subtract [that number] from the squared base number, and whatever remains we divide to ten, which is two less than the base number. The result is the number of the first person who had multiplied by two, and what remains is the number of the second person, and the total of these two numbers taken the base number is the number the third person had.
An example: Three numbers are hidden between three people, of which the total is twelve, and this number is the base. So we multiplied this number by twelve and we got one hundred forty-four, which is the base number squared. So we told one person, “Whatever you have, multiply by two,” and told the other person, “Whatever you have, multiply by elven,” which is one less than the base number, and told the third person, “Whatever you have, multiply by twelve,” which is base number. When they have done this, we ask what the result is. They say one hundred and twenty. We subtract this from one hundred and forty four and twenty-four remains. We divided that by ten, which is two less than the base number, and the result was two, and what remained was four. We said that two is the number of the first person, whom we told, “Multiply your number by two,” and the remaining four is the number of the person whom we told to multiply by eleven. Four added to two and [this] subtracted from twelve is six, which is the number of the third man, whom we told to multiply by twelve.
[This trick can be used to reveal a three chosen cards where the sum of the three numbers are twelve.]
Another type: The same number game can be done and it is nice. [You] Should bring a handful of peas. Take out ten peas and give them to three persons, so that everyone hides as many as he wants. When they have done so, put one hundred peas on a plate, because it is ten peas that have been given out and should be ten times that. [Then tell the first person,] “Take two times as many as you have [secretly from this plate] and give it to the fourth person.” When he has given [the peas to that person], tell the second person, “Take nine times as many as you have and give it to the [Text has been dropped here. It should read: fifth person.” When he has done this, tell the third person, “Take ten times as many as you have and give them to the] sixth person.” When they have, from whatever is left on the plate, take out eight peas each time, and count how many [groups of] eight peas you took out, and that is the number of the first person who gave two times [his number of peas] to the fourth person. Then the fourth person is told, “You have two times as many as that.” Whatever is left on the plate, that is the number of the second person, and the fifth person has fifteen [sic; should be “nine”] times that, and the total of the first person and the second person subtracted from ten is the third person’s, and the sixth person has ten times that. And all is that way [i.e., all work the same way”
[Another type:] If a group is gathered, and asks how to connect three sticks at three points so as to obtain nine segments, how should it be done? If we want this, the way of connecting is to make a triangle, so that the three points [of contact] are made. So with the points we make, we obtain nine segments, in this way:
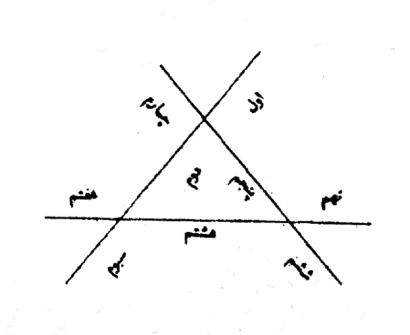
And if they say that we want to divide three sticks on two points to create seven segments, how should it be done? They should put one stick on the side of two sticks the way we have shown to make two connection points. So for the connection points we get seven segments, as we have shown:
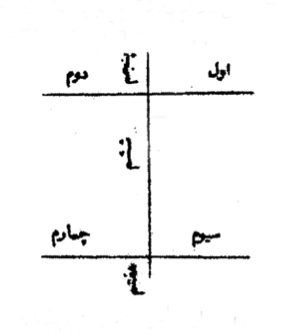
And if they say, “We want to connect four sticks so that they are divided into twelve segments,” how should it be done? We reply that we make a rectangle, so that four connection points are formed the way we have shown. So we make connection points until it is divided into twelve pieces as we have shown.
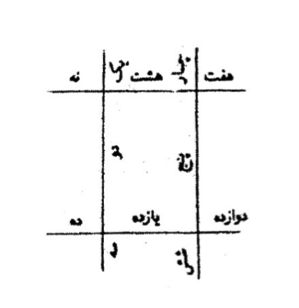
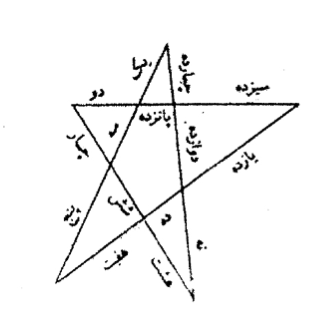
And if they say, “We want to connect five sticks at five points, so that they are divided into fifteen segments,” we say we make a pentagon from the five pieces the way we have shown, in which there are five connection points, and with these points of connection fifteen segments are made, and all is the way we mentioned.
There is a city with a perimeter of sixty parsangs [roughly equivalent to three miles] and it has twelve gates. So the king of the city sent out seven courtiers along the road. He told the first courtier go one parsang each day. [He] told the second to go two parsangs each day. [He] told the third to go three parsangs each day. [He] told the fourth to go four parsangs each day. [He] told the fifth to go five parsangs each day. [He] told the sixth to go six parsangs each day. [He] told the seventh to go seven parsangs each day. “Go around the city at the rate I told you. When all seven of you get to the gate, let me know.” They went around the city and all arrived at the gate at the same time. How should we find out how many times each had gone around the city and how many days each one took to get there.
So the man who traveled seven parsangs each day has travelled fourteen times around the city, during one hundred and twenty days. The one who traveled six parsangs each day has traveled twelve times around the city during one hundred and twenty days. And the one who traveled five parsangs each day has traveled ten times around the city during one hundred and twenty days. And the one who traveled four parsangs each day has travelled eight times around the city during one hundred and twenty days. And the one who traveled three parsangs each day has traveled six times around the city during one hundred and twenty days. And the one who traveled two parsangs each day has traveled two times around the city during one hundred and twenty days and had arrived there [at the gate].
[Notice that Tabari has calculated two rounds for the first person, and so for the rest of the courtiers the number of rounds around the city and the distance they traveled is doubled.]
There are three different pieces of land that must be sold: one is ten parcels, one is thirty parcels and one is fifty parcels. All [must be sold] at the same rate, in such a way that all three have the same price. How should we find out how they are sold since, to be sold since, if each parcel of the smallest [piece of land] is sold for one dirham [a silver coin], ten dirhams are gained. And if the thirty parcels has to be sold one parcel for a dirham, thirty dirhams are gained. And if the fifty parcels have to be sold one parcel for a dirham, fifty dirhams are gained, and they are not all at equal prices; and if [they] sell the smallest for a dirham, the thirty parcels will be three dirhams and fifty parcels will be five dirhams, and they are not equal. The solution is that when the customer comes, the seller should say, “I will sell every seven parcels for one dirham, and whatever parcels are left, I will sell for three dirhams a parcel.” So if he does this, the price and rate of all are equal. He has to sell seven parcels of the ten parcels for a dirham; three parcels are left, which sell for three dirhams each; and ten dirhams are gained. Each [group of] seven parcels of the thirty parcels is sold, and four dirhams is gained from the four lots of seven parcels; and what is left will be sold for three dirhams per parcel, which is six dirhams, for a total of ten dirhams. And each [group of] seven parcels of the fifty parcels is sold for one dirham. From the seven lots of seven parcels, seven dirhams are gained. One parcel is left from the fifty parts, the price is three dirhams, and total will be ten dirhams. So all the three prices are equal.
Another is that three men were travelling on the road. One had three loaves of bread. And one had two loaves of bread, and the third had no bread. When it came time to eat, they sat and ate all those five loaves of bread so that nothing was left. The man who did not have bread asked them, “How much bread did you have?” They said, “Five loaves of bread.” That man gave five dirhams to those two men and said each [should] take the price of his bread. The man who had two loaves of bread told the other man, “You had three loaves of bread, take three dirhams; and I had two loaves of breads and I will take two dirhams.” The owner of three loaves of breads said, “My share of dirhams is more,” and there arose an argument between them. How much should each man get?
The solution to this is that the one who had three loaves of bread gets four dirhams, and the one who had two loaves of bread gets one dirham. Because they eat equal portions of the bread, four pieces of one third of a loaf of bread of the person who had three loaves of bread are eaten by this man [who is paying], and one third from the person who had two loaves of bread. So the man who paid the dirhams has eaten five pieces of one third of the loaves of bread and has given five dirhams; for every third of a loaf of bread one dirham, and for four pieces of one third of a loaf of bread four dirhams, and for a third of a loaf of bread a dirham; and the solution is [had] in this way.
[Since there are five loaves of bread and each is divided into three pieces, there are fifteen pieces total. The three men eat the same number of pieces, which must be five pieces. The owner of the three loaves eats five of his nine thirds and gives the man without bread his remaining four third. The owner of the two loaves eats five of his six thirds, leaving just one third for the man without bread. The five dirhams are therefore distributed four to the man with five loaves and one to the man with two loaves.
The kings of two cities sent two courtiers to each other. One king told his courtier to go one eighth of the total distance from this city to the other city every day. And the other king told to his courtier to go one tenth of the distance from this city to the other city. Now, how should say how many parsangs it was from this city to the other city, and how many parsangs did each one have to travel, and on which day did these two courtiers reach each other?

An example of this is that we get a number that is divided by eight and ten, and that is forty, wherein five is one eighth of it and four is one tenth of it. So we add both [five and four], which is nine. We divide forty, which is the base number, by nine, which is four with a remainder of four. And nine is the number [of days at which] the two couriers have met. So we multiply four in the five which is one eighth [of forty] we get one hundred and sixty. This is the amount of the distance gone by the man who has traveled one eighth of the distance. And an eighth of each day [traveled] is forty-five, and one tenth of [each day] is thirty-six. And the distance between this city and the other city is three hundred and sixty parsangs, when both are added together.
[The time of the travel multiplied by the speed of both couriers will be equal to the distance between two cities. In other words, the time of the travel multiplied by the sum of one eighth and one tenth will be equal to the distance between the two cities.]
Chapter Thirty-four is the last and perhaps the most important: “On finding the fundamentals of the book.” This chapter shows the levels of science and philosophy in Persia at his time. It starts with “Most people are those who would not believe in what is in this book, because they do not know, and when they hear about it, they wonder.
“And some are those look down and say: There is not truth in it. And there are those who experiment without knowledge and education, and never use tools, and things do not work for them and they are not aware of the misfortunes and causes that have affected the drugs, and they do not think about the cause of it.”
This thought defines a scientific approach from those of the disorganized, dogmatic and superstitious. He goes on to list various miracle workers of the time, but gives no credence to their claims:
“It has been known that that these things can be done. For example, there is Abdullah ibn Helal, who claimed that with his sleight-of-hand, “Whatever miracles Jesus claimed to do, I can do.” And it is said that he walked on the water and flew on the air. And another was Saleh Madani. The best effects of his knowledge and skill and industry were that he took the dirhams from the bags of money changers and opened the [treasure] chests with spells. And another was Abdullah ibn Meimoon. His finest knowledge was that for each city he wanted to go, he drew a picture, then stepped [magically] into that city and claimed to be an Imam, and Shiites accepted him. And another was Bu Khalid Kabuli. And his work and deeds were that he changed the behavior of animals with the food or drink he gave them. And another was Erb, who could disappear from the sight of anyone he wished and go to anyone who wanted. And another was Arruf Yamama. And, when he wished, could bring near himself [anything] from the seven continents. And it is said he threw a ring into a large washing bowel [of a particular type, round and shallow, made of tine-plated copper, in which clothes were washed] and went into it and nobody saw him. And the other one was Shamuel who cast spells on perfumes and oils, and to whomever he gave them they were charmed and fell under his spell. And another was Abdus Babeli, who made a picture and put it beside him, and drew an arrow and a sword in the hand of the picture, and signaled that in such a city or at such a place that a person would be hit, and he inflicted that wound on the face of another picture in front of him. If he hit the eyes [of the picture], the eyes of the person were hit, and if he hit the head, the head of the person was hit, whether the person was far away or close. And there was Bu Khalid Khorasani who was the master and leader of all, and claimed amongst the Shiites, “I am the successor of Hussein ibn Ali as Imam,” and also claimed divine knowledge that “Whatever Jesus, son of Mary, did, I can do as well.” Listing the names of all these people takes times. But the point is that, whoever has toiled for knowledge has not wasted [time]. And many of them were not successful, such as Mosailama the liar, and Taliha and Ansi; and it is said Hallaj was one of them, and Abulhasan Kufi and Taleghani and Abdolsamad and Abdolhamid and Mehrabadi and Kermani and the like. If the properties of things are not fully understood, and if someone doubts these things, this knowledge is not for him, since the wise man is he who can deduce a lot from a little and from the surface to the depth and from the present to the absent.”
Some of these men were famous mystics, religious leaders and holy men, to whom followers believed faith had given miraculous powers. Since Tabari was familiar with conjuring methods, he rejected the claims of spiritual or supernatural abilities for them and classified all their deeds as trickery, learned by effort. After giving some examples of strange things, he continues: “If learned men have done something, and you do it and it is not like their work, or it is corrupted, or you could not do it because of going from one thing to another thing, it may not happen. Put the blame on yourself, so that you always be a seeker”. He goes on to list many more strange things that are difficult to believe, and then closes the book with:
“And there is no end to these thing and all cannot be mentioned, but this much, which has been said, is enough.”
- Tuhfat al-Ghraib by Muhammad ibn Ayyub Alhaseb Tabari, ed. Jalal Matini, Second edition 2014, Library, Museum and Document Center of the Islamic Republic of Iran Parliament, 508 pages.






